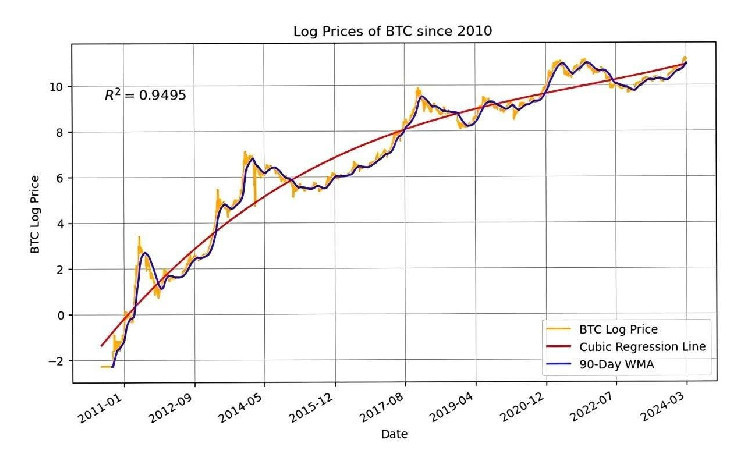
What if Bitcoin keeps on its current trajectory of near-exponential growth? To put this in perspective, consider the chart of the logarithm of Bitcoin's price, and let’s forecast it forward. I'm calling this approach the exponential model because I am taking the natural logarithm of the Bitcoin price, and then applying the exponential operator to reverse out the predicted price. Logarithms are useful tools for linearizing exponential phenomena, and Bitcoin's price is one example of such a phenomenon. A phenomenon with exponential growth will look roughly linear in logarithm space, so that chart looks like:
The data runs for the last 13+ years. The orange line is the log of the Bitcoin price, the black line is the 90-day weighted moving average (WMA) of the logged Bitcoin price, and the red line is the curve of best fit. The purpose of the moving average is to smooth out the short-term volatilities in Bitcoin price and expose some of the longer cycles.
To fit the curve, I found the best cubic equation that fit the data. The decision to settle on a cubic rather than quadratic function or even higher order polynomial is somewhat arbitrary. The truth is you can always overfit data by using a high-order polynomial. The problem is that it will have extremely high in-sample predictions but questionable out-of-sample predictions. A cubic has slightly more flexibility than the quadratic, but not so much that no one believes it. Ultimately, the goodness of fit measure of 0.9492 is extremely tight, where 1 is a perfect fit.
 forbes.com
forbes.com